a) 2x = 8
b) 2x = 64
c) 25x = 125
e)
2)Determine o conjunto verdade das seguintes equações exponenciais:
a) 3x+1 + 3x+2=12
b) 2x +1 + 2x + 3 =20
c) 7x-1 +7x+1=50
d) 5x-1 +5x-3=26
3)Determine o conjunto verdade das seguintes equações exponenciais:
a) 22x – 9.2x + 8 =0
b) 4x – 3.2x + 2 =0
RESPOSTAS:
1) Questão:
1º tipo de resolução:
Para resolver esse tipo de equações exponenciais as bases devem ser iguais, para isso igualamos as bases.a)
2x = 8 (fatorando o 8 para igualar as bases);
2x = 23 (agora igualando os expoentes);
x=3
s={3} ( solução ou conjunto verdade)
b)
2x = 64 (fatorando o 64 e igualando as bases);
2x = 26 (igualando os expoentes);
x=6
s={6}
c)
25x = 125 (fatorando os dois membros para igualar as bases )
(52)x = 53 (igualando os expoentes)
2x = 3
d)
7x = 343
7x = 73
x= 3
s={3}
e)
2x = 2-5
x= -5
s={-5}
2) Questão
Estudem as propriedades das potências: (am .an = am+n)
a)
3x+1 + 3x+2=12 (separando cada termo com potência de mesma base);
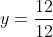
y=1 (substituindo y=1 para obter o valor de x)
3x= y
3x = 1
c)
7x-1 +7x+1=50

2) Questão
2º tipo de resolução:
Trocamos uma variável (letra) por outra variável, que chamamos de mudança de base.Estudem as propriedades das potências: (am .an = am+n)
a)
3x+1 + 3x+2=12 (separando cada termo com potência de mesma base);
3x . 31 + 3x . 32=12 ( troco 3x por uma letra qualquer. Usando y, ficando assim: 3x= y);
y . 31 + y . 32=12 (substituindo na equação y por 3x );
3y + 9y = 12
12y = 12
y=1 (substituindo y=1 para obter o valor de x)
3x= y
3x = 1
3x = 30
x= 0 (igualando os expoentes)
s={ 0}
b)
2x +1 + 2x + 3 =20 (separando cada termo com potência de mesma base);
2x . 21 + 2x .2 3 =20 ( trocando 2x por y, ficando assim: 2x= y);
y . 21 + y .2 3 =20
2y + 8y = 20
10y = 20
c)
7x-1 +7x+1=50
7x . 7-1 +7x. 71=50 ( substituindo: 7x =y )
y . 7-1 +y. 71=50
7x =y
7x=7
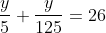
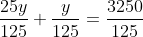
26y = 3250
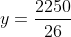
y= 125
5x =y
5x = 125
5x = 53
x = 3
s={3}
3) questão:
a)

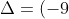%5E%7B2%7D-4.1.8)





2x = p fazendo a substituição
2x = p'
2x = 8
2x = p''
2x = 1
7x=7
7x =71
x=1 (igualando os expoentes)
s={1}
d)
5x-1 +5x-3=26
26y = 3250
y= 125
5x =y
5x = 125
5x = 53
s={3}
3) questão:
3º tipo de resolução:
Além, de fazer a troca de um variável por outra variável ( mudança de base) resolver-se a equação do do 2º grau.a)
22x – 9.2x + 8 =0
(2x)2 – 9. 2x + 8 = 0 ( 2x = p )
p2 – 9. p + 8 = 0
2x = p fazendo a substituição
2x = p'
2x = 8
2x = 23
x= 3
2x = 1
2x = 20
x= 0
s={0, 3}
b)
4x – 3.2x + 2 =0
(2x)2 – 3. 2x + 2 = 0 ( 2x = p )
(p)2 – 3.p + 2 = 0
2x = p
2x=p'
2x=2
2x = 21
x=1
2x=p''
2x=1
2x = 21
2x = 20
x=0
s={0, 1}
c)
25x – 30.5x = -125
(5x)2 – 30. 5x + 125 =
0 ( 5x = p )
(p)2 – 30.p + 125 = 0
5x = p
5x = p'
5x = 25
5x = 52
x = 2
5x = p''
5x = 5
5x = 51
x = 1
S={1, 2}
Agora é com vocês:
1) resolva as equações exponenciais:
a) 4x=16
b) 25x = 625
c) 2x+2 + 2x-1 = 18
d) 4x – 12. 2x = - 32
Respostas:
a) s={2}
b) s={2}
c) s={2}
d) s={2,3}

